Step 79: Explore CS1 Grading

At the end of every semester, and especially the last two when I’ve taught CS1, I always have the same thoughts about grade inflation and the meaning of grades. This is a particular problem for CS1 because somewhere between a third and a half of the students get A-‘s or A’s – a much larger proportion than in other introductory courses. One possible interpretation is that I grade too easily, but other interpretations are possible. Two in particular come to mind:

• The course structure allows students to get objectively higher grades. I’ve written about the lack of exams and the frequent, low-stakes grading structure. I also allow unlimited autograder submissions, which means that students can tweak their code until they pass all the test cases. The autograder also provides immediate feedback, which leads to…

• Students spend more time on this class. The data from the end-of-semester teaching evaluations support this: over both semesters (59 respondents total), the median and average time spent on this course outside of the classroom is 6 and 8.4 respectively. Keep in mind that this course already has 6 hours of lectures and labs per week, and that a course is supposed to take about 10 hours total.

(This plot omits one student who reported spending over 40 hours per week on this course. I really hope they were exaggerating.)

The real answer to the high grades is likely some combination of all three explanations. What I can’t decide is what this means in terms of the grading structure of the course. I am less concerned about grade inflation than I am about the distribution of grades. I wrote in the previous post that my “quizzes” are tri- or quad-modal. It turns out that my final grades are not as bad, but are still bi-modal, with peaks around 85% and 95%.

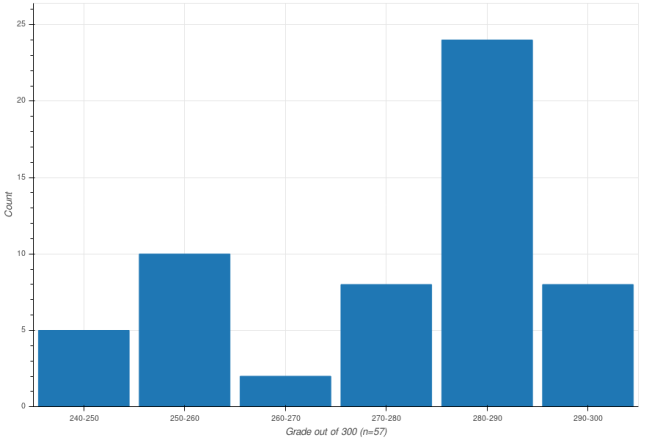
(Grades lower than B- have been omitted.)

As with grade inflation, there is the question of what this means, and there is the meta-question of whether it is problematic. The face-value explanation would that there are two groups students – one that gets computer science, and one that doesn’t. I’m undecided whether this describes the “true” distribution of computer science competency, but philosophically as a teacher I should not design courses with this assumption. If instead I take for granted that student skill levels are unimodal, then what the grade distribution would suggest is that I am not sufficiently sensitive to students some middle section of that curve.

One thing I do know is that this is not a problem I can fix by changing the grading structure but keeping the same assignments. I know this because I have iterated through the space of assignment weights. Within the constraints of low-stake assignments, no set of weights would transform the existing grades of my students into a unimodal distribution peaking around B or B+. What this means to me is that if I am indeed failing to identify the B+ students, the place to start would be to look at the actual content of the assignments.

I don’t have a takeaway from this. I dislike the bimodal distribution of grades, but it’s unclear whether I am justified in my dislike, and even if so, what I can do to change it. Assigning grades, as well as deciding on the grading structure of a course, requires thinking through not just what students should learn and whether their grade reflects that, but also how we trade off student achievement, time spent, and the value of negating institutional grade inflation. As a final thought, it has occurred to me that perhaps grades are not the venue to demonstrate these nuances. Perhaps grades should be seen only as the carrot-and-stick, with more emphasis put on detailed feedback provided through other channels.

Step 78: Assign Essays in CS1

As the semester wraps up, I found myself in the strange position of grading three sets of essays for my introductory computer science class.

1. The first essay is what I called the “How to Computer” essay. Specifically, the prompt asked students to explain what it means “for everything to be ones and zeros, from numbers to videos to programs themselves”, and “what is actually happening when you run the code that you write”. This assignment served as the culmination of two weeks of lectures, starting with memory, then parsing, computer systems, and finally assembly. It’s my first time teaching this material, and I have more thoughts on this which I’ll share in a later post.

2. The second essay is for the students’ final project, which is broadly defined structured around data journalism. Their assignment was to find a public dataset, answer a question about it with programming, then write up a report. Specifically, they must answer:
   • What dataset you used and what the dataset describes
   • What question you asked and why it’s an interesting question
   • What your predicted answer was, before you wrote code
   • The tricky part(s) to answering your question (if appropriate)
   • What your code suggests the answer is
   • Reasons why your answer may be incorrect
   • Additional questions that you might ask in the future

3. The third essay, for extra credit, is an edited paper on diversity. Specifically, I asked students to write about ways to attract diverse students to computer science. In retrospect, I should have been a lot more specific, but asking for actionable strategies for recruiting women and minorities to computer science at Oxy.

I will be honest and say that all three assignments were unplanned – that is, I was not deliberately seeking to incorporate writing into my course. The extra credit essay had the longest history – it has been in the syllabus since the beginning, and was partially inspired by the experiences of my students. The others, however, were mostly spur-of-the-moment decisions as I struggled to find sufficiently interesting assignments. It’s worth nothing that the three assignments are different in both prompt and response. The computer organization paper provides minimal direction and asks students to regurgitate lecture material within a larger framework; the data journalism paper is much more focused in context, but much broader in content; and the diversity paper requires research and editing. I was surprised that the last paper had the highest quality, even by the first draft – my hypothesis is that it’s the closest in style to the other papers that the students have written (not to mention the self-selection for extra credit).

I think these first attempts were in the right direction, and I like the idea of making students write in a computer science course. That said, I’m not happy with how I support student writing. Both required papers could use an editing process, and I wish I had stayed at a higher level when I edited the extra credit paper. The main constraint is scheduling – it’s hard to find a week in the semester for this revision process, and harder still to teach anything substantial about writing. I will have to remember this when I teach this course again next year.

Step 77: Practice Practicum

The semester is wrapping up, and the first course to “conclude” is the Practicum course. There was no final presentation; instead, the last community partner meeting was on Saturday, where the students demo’ed their work… and that was that. There are some small changes we still have to do, and I will be back with some students next week to set up a production system, but the course is over.

Since this is the first time I’ve taught the course, I thought I would share some lessons learned. As a reminder, we were building a system that allowed volunteers with no tech experience (as in, may need help creating an email account) take pictures, then have it be OCR’ed and made searchable online.

• Setting up expectations is (as expected) key. I knew this going in, and still failed to convey that we were not building a mobile app for the pictures. This mismatch was discovered three months into the four-month project. Lucky for us, this expectation mismatch did not require starting over, and I think the conversation we had in fixing this led to a better program at the end. Given that I was already watching for this problem and it still happened, I’m not sure what I should do next time to avoid it.

• Students need help with organizing larger code bases. This lesson may be specific to me, because I was working with students who have only finished CS1. The insidiousness of this lesson is that the code works – it just repetitive, with multiple functions that do similar things, and the entire codebase difficult to extend for new functionality. I ended up re-writing a significant portion of the code about halfway through the semester, but in the future I will require code reviews and refactors. Similarly…

• Force students to write documentation. By documentation here I don’t mean comments or APIs, but a narrative of the design process. I would like records of what ideas they have considered and why they ultimately decided on their current solution, but getting them to write this report was like pulling teeth. I assigned weekly reflections, which worked at the beginning of the semester when they were still understanding the problem, but were less useful as the coding took precedence. Even then, the reflections do not address the technical decisions. Both the previous point and this one lead to…

• Breaking down grades is futile. I started the semester with a grade breakdown, with some percentage of student grades for peer evaluations, community partner evaluations, report, code, etc., but it’s unlikely I will grade based on anything but instinct. I talked to a colleague about their community-based learning class, one that is similarly product-focused, and they told me that they start with a baseline of A’s and subtract from there. I’m not opposed to this strategy, but also find it unsatisfactory. At the same time, it’s hard to devise any objective measure of goodness, even if the grade is broken down, so it seems like it comes down to gut judgments regardless.

• Be prepared to provide ongoing support. This is tricky; students have no formal ties with the project after the semester, and even if they are willing to support the code, I feel bad putting them on the hook. As a trial run of the course, this current project is simple enough that I can support it, but I’m not sure how it would scale up when projects get more complicated or when there are more projects to be supported.

I deliberately imposed as little structure as possible on the students this semester, and it has helped me see where things break down. I was able to pick my students, and having their trust helped prevent the class from failing as I figured things out. If I teach this course again next year, it will be with more students and more projects. The library we worked with this semester agreed to work with us again (which is honestly very validating), but I will need to find new community partners as well. In the meantime, let’s see if I can put together a more coherent and structured course.